Having a Lenovo Y500 laptop with good specs (8GB RAM, 4 processors) that runs on Windows 7 made me feel limited when it came to scientific computing. Unix based systems like Linux and Mac OS are more convenient to use than Windows systems. As a result, after doing some research I decided to install a Linux distribution Ubuntu 16.04 aka Xenial alongside my Widnows 7 OS. This gives me the option to boot any of the two. I heavily use Python 2.7, 3.5 and R which I all install on my new Ubuntu partition. Below are the steps that worked for me. Hopefully, you find them useful.

Tabe of contents

• Dual Boot Windows 7/8/10 and Ubuntu 16.04 Xenial
  • Create Bootable USB
  • Partition Hard Drive
  • Boot from USB and Install
• Install R
• Install Rstudio
• Install Git
• Install Python 2.7 and 3.5 (Anaconda distribution and virtual environment)
  • Instal Anaconda Python 2.7
  • Install Anaconda Python 3.5 virtual environment
• Install Sublime Text 3

Dual Boot Windows 7/8/10 and Ubuntu 16.04 Xenial

Create Bootable USB

You will need to have

• Ubuntu 16.04 ISO
• Rufus to create a bootable USB Device
• A USB device with at least 8GB space

You can start with burning the Ubuntu ISO onto the USB drive using Rufus. Just launch Rufus choose the ISO, the USB drive and press the start button. Now, you have a bootable USB drive with Ubuntu 16.04.

Partition Hard Drive

Now, we need to create free space on the HD for the Ubuntu 16.04 to be installed on. There are a lot of guides online and I present the way that worked for me. I use the Windows default app diskmgmt.msc. Just search for it and launch it. Choose the hard disk with the most free space on it. Right click on it and choose shrink option. You only have to shrink it by 20GB. It is enough for Ubuntu 16.04 and 18GB of storage for your files. You can go above 20GB of course. That’s it. At this point we can boot Ubuntu Xenial and install it if we like it.

Boot from USB and Install

taken from ubuntu.com

Whatever laptop you have bring up the boot menu on startup. For me (Lenovo Y500) there is a button on the left behind the power plug. In the boot menu you should see an option for a USB drive. Boot from the USB and you will see

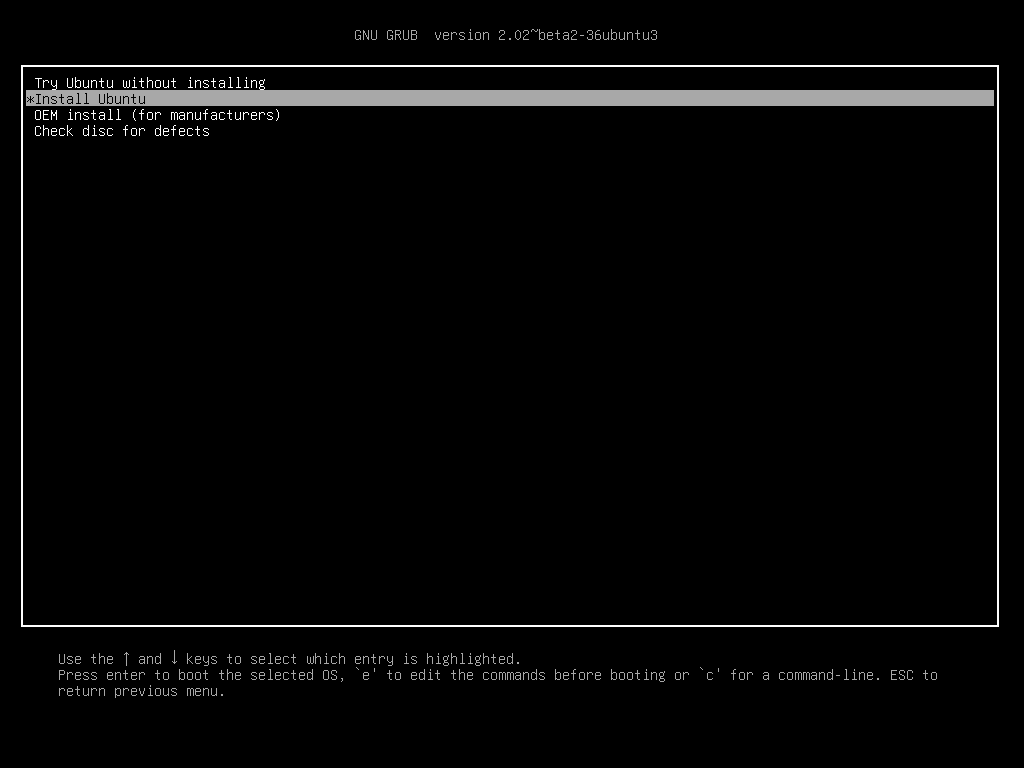
You can try Ubuntu Xenial out first by going with the first option (Try Ubuntu without installing). Once you are convinced it is great (more convenient than Windows for data purposes at least), shutdown, boot from USB again and install it. At some point you will see this

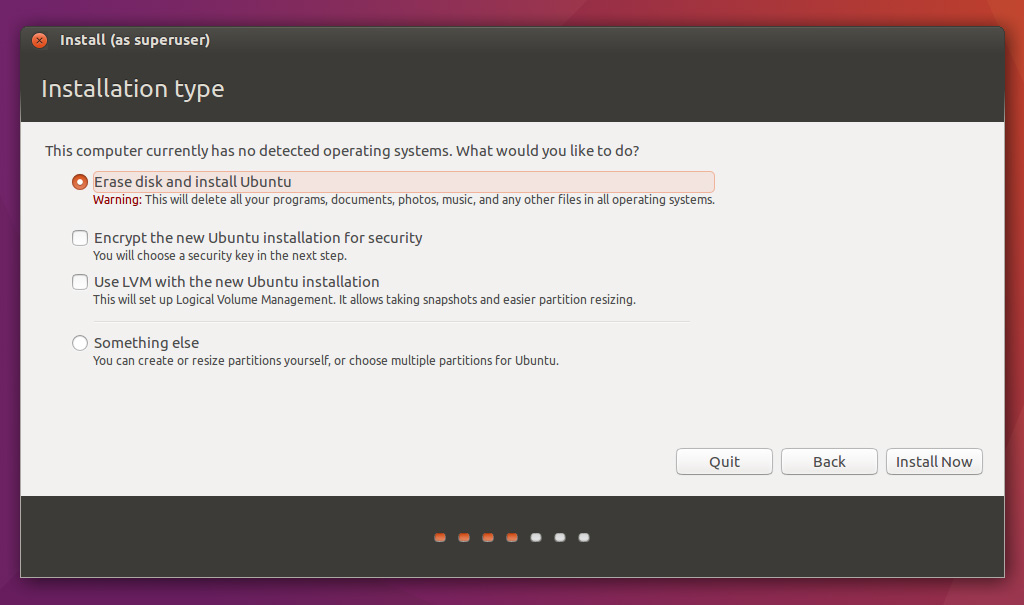
Normally, after you shrank one of your partitions and allocated free space of 20GB or above there should also be an option Install alongside Windows. If you do not see it after going through previous steps let me know and I will look into it.

Finally, once installed run in terminal

sudo update-grub

This will update the boot loader menu and nexxt time you see boot menu you will be able to choose Ubuntu or Windows. Lets move on to installing statistical software.

Install R

To install R on Ubuntu 16.04 aka Xenial execute the below commands in terminal.

taken from Stackoverflow

sudo add-apt-repository ppa:marutter/rrutter
sudo apt-get update
sudo apt-get install r-base r-base-dev

Install Rstudio

Now, that we have R installed lets get Rstudio.

taken from R-Bloggers

sudo apt-get install gdebi-core
wget https://download1.rstudio.org/rstudio-0.99.902-amd64.deb
sudo gdebi -n rstudio-0.99.902-amd64.deb
rm rstudio-0.99.902-amd64.deb

Install Git

sudo apt-get install git

Install Python 2.7 and 3.5 (Anaconda distribution and virtual environment)

We will install Anaconda 2.3 Python distibution and then create a virtual Python 3.5 environment using conda.

Instal Anaconda Python 2.7

First, install Anaconda 2.3 which is based on Python 2.7 .

taken from Stackoverflow

wget https://3230d63b5fc54e62148e-c95ac804525aac4b6dba79b00b39d1d3.ssl.cf1.rackcdn.com/Anaconda-2.3.0-Linux-x86_64.sh

bash Anaconda-2.3.0-Linux-x86_64.sh
rm Anaconda-2.3.0-Linux-x86_64.sh

You will be promted to read the user agreement and set some parameters during installation. Go through it and once the installation is finished run below commands and you will see something like this.

koba@kobakhit:~$ exec bash
koba@kobakhit:~$ python
Python 2.7.10 |Anaconda 2.3.0 (64-bit)| (default, May 28 2015, 17:02:03) 
[GCC 4.4.7 20120313 (Red Hat 4.4.7-1)] on linux2
Type "help", "copyright", "credits" or "license" for more information.
Anaconda is brought to you by Continuum Analytics.
Please check out: http://continuum.io/thanks and https://binstar.org
>>> exit()

Type exit() and enter to get back to bash.

Install Anaconda Python 3.5 virtual environment

Anaconda is installed and is the default python executable. Second, lets create Python 3.5 virtual environment. Below info is taken from a concise cookboook.

To install a virtual python environment you want use this command template conda create -n yourenvname python=x.x anaconda. For example, I created a virtual python 3.5 environment called tpot. For a list of available python versions type conda search "^python$".

conda create -n tpot python=3.5 anaconda

To activate and deactivate your virtual environment type

source activate tpot
source deactivate tpot

# remove a virtual enironment
conda remove -n tpot -all

Now, you have Python versions 2.7 and 3.5 with all the Numpy, Scikit-Learn, Pandas, etc. packages already installed thanks to Anaconda distribution. As a finishing touch lets install jupyter to work with IPython notebooks.

conda install jupyter

You will have to install one for your virtual environment as well. Recall, I created a virtual env called tpot previously. You might need to close and reopen the terminal for the source activate to work.

source activate tpot
conda install jupyter
source deactivate

To start IPython run jupyter notebook which will create a tab in your browser.

Install Sublime Text 3

This is my choice of text editor.

taken from Stackoverflow

sudo add-apt-repository ppa:webupd8team/sublime-text-3
sudo apt-get update
sudo apt-get install sublime-text-installer

Conclusion

There are several distros created for scietific computing that have some software preinstalled. To name a few

• Bio-Linux
• Poseidon Linux
• Fedora Scientific

For software highlights of each you can refer to this article. I can promise you that none at the moment of writing had all the software I wanted installed (R and Rstudio, Anaconda Python 2.7 and 3.5). Until somebody releases a data science Linux distro Ubuntu Xenial is the most optimal choice in terms of flexibility and convenience.

Bonus

Install Jekyll (static website generator)

sudo apt-get install jekyll

A simple example of visualizing geoson data in python using Folium. We obtain Philly Indego bike data from opendataphilly website. We download the data using the website’s free public api.

import json,urllib2
import pandas as pd

# add a header so that the website doesnt give 403 error
opener = urllib2.build_opener()
opener.addheaders = [('User-agent', 'Mozilla/5.0')]
response = opener.open('https://api.phila.gov/bike-share-stations/v1')

# parse json using pandas
df = pd.read_json(response)
df.head()

Now, df is a dictionary of dictionaries. We are interested in the features column. Each entry looks like this.

df['features'][0]

{u'geometry': {u'coordinates': [-75.16374, 39.95378], u'type': u'Point'},
 u'properties': {u'addressCity': u'Philadelphia',
  u'addressState': u'PA',
  u'addressStreet': u'1401 John F. Kennedy Blvd.',
  u'addressZipCode': u'19102',
  u'bikesAvailable': 6,
  u'closeTime': u'23:58:00',
  u'docksAvailable': 19,
  u'eventEnd': None,
  u'eventStart': None,
  u'isEventBased': False,
  u'isVirtual': False,
  u'kioskId': 3004,
  u'kioskPublicStatus': u'Active',
  u'name': u'Municipal Services Building Plaza',
  u'openTime': u'00:02:00',
  u'publicText': u'',
  u'timeZone': u'Eastern Standard Time',
  u'totalDocks': 25,
  u'trikesAvailable': 0},
 u'type': u'Feature'}

# number of rows (bike stations)
len(df["features"])

73

We organize data first before plotting to follow a Folium example. Basically we need to create a list of tuples with latitude and longtitude. We called it coordinates.

# Organize data
coordinates = []

for i in range(0,len(df['features'])):
    coordinates.append(((df["features"][i]["geometry"]['coordinates'])))

# convert list of lists to list of tuples      
coordinates = [tuple([i[1],i[0]]) for i in coordinates] 
print(coordinates[0:10])

[(39.95378, -75.16374), (39.94733, -75.14403), (39.9522, -75.20311), (39.94517, -75.15993), (39.98082, -75.14973), (39.95576, -75.18982), (39.94711, -75.16618), (39.96046, -75.19701), (39.94217, -75.1775), (39.96317, -75.14792)]

Let’s visualize the coordinates geoson data using Folium.

import folium
import numpy as np

#print(folium.__file__)
#print(folium.__version__)

# get center of map
meanlat = np.mean([i[0] for i in coordinates])
meanlon = np.mean([i[1] for i in coordinates])

# initialize map
mapa = folium.Map(location=[meanlat, meanlon],
                  tiles='OpenStreetMap', zoom_start=13)
# add markers
for i in range(0,len(coordinates)):
    
    # create popup on click
    html="""
    Address: {}<br>
    Bikes available: {}<br>
    Docks: {}<br>
    """
    html = html.format(df['features'][i]['properties']['addressStreet'],\
               df['features'][i]['properties']['bikesAvailable'],\
               df['features'][i]['properties']['docksAvailable'])
    iframe = folium.element.IFrame(html=html, width=150, height=150)
    popup = folium.Popup(iframe, max_width=2650)
    
    #  add marker to map
    folium.Marker(coordinates[i],
                  popup=popup,
                 ).add_to(mapa)

mapa # show map

We can cluster nearby points. Also, let’s look at a different background by changing the tiles argument. List of available tiles can be found in Folium github repo.

from folium.plugins import MarkerCluster # for marker clusters

# initialize map
mapa = folium.Map(location=[meanlat, meanlon],
                  tiles='Cartodb Positron', zoom_start=13)

# add marker clusters
mapa.add_children(MarkerCluster(locations=coordinates, popups=coordinates))
mapa

We can utilize Folium plugins to view the geoson data in different ways. For example, let’s generate a heat map of the bike stations in Philly. We can see that there are dense areas in center city and Chinatown mostly.

from folium.plugins import HeatMap

# initialize map
mapa = folium.Map(location=[meanlat, meanlon],
                  tiles='Cartodb Positron', zoom_start=13)

# add heat
mapa.add_children(HeatMap(coordinates))
mapa

For more examples go to the Folium’s examples page.

Resources used

• Folium docs
• Folium Github

We try to use Integer Linear Programming to build a perfect 25 men roster baseball team. We present our best team below which is the solution of the ILP model we built using the 2015 MLB season player data. If you understand baseball please evaluate our resulting baseball team and drop a comment, so that we know whether ILP can be used to get a decent baseball team. After the table I describe how we arrived at our solution.

Edit: The choice of statistics for our utility index is almost random. The main goal was to model the general constraints and objective function. This code allows to easily add desired statistics and extend the general case to include more sophisticated preferences, for example using the weight vector.

Prerequisites

To follow the process of us setting up the ILP model you should have familitarity with

• Linear algebra
• Linear optimization
• Integer programming

Data preprocessing

Let’s read in the 2015 regular season player level data.

dat = read.csv("Baseball Data.csv")
head(dat[,1:4])

##     Salary              Name      POS Bats
## 1   510000      Joc Pederson       OF    L
## 2   512500      Stephen Vogt       1B    L
## 3  3550000      Wilson Ramos        C    R
## 4 31000000   Clayton Kershaw       SP     
## 5 15000000    Jhonny Peralta       SS    R
## 6  2000000 Carlos Villanueva Reliever

The dataset has 199 rows (players). There were NA's for some players and their game statistics which we replaced with 0. The reason we replaced the missing data with zeros is that when we construct the player utility index missing data won’t count towards or against players.

dat[is.na(dat)] = 0

Each baseball player has game statistics associated with them. Below is the list of player level data.

names(dat)

##  [1] "Salary"   "Name"     "POS"      "Bats"     "Throws"   "Team"    
##  [7] "G"        "PA"       "HR"       "R"        "RBI"      "SB"      
## [13] "BB."      "K."       "ISO"      "BABIP"    "AVG"      "OBP"     
## [19] "SLG"      "wOBA"     "wRC."     "BsR"      "Off"      "Def"     
## [25] "WAR"      "playerid"

You can see the statistics description in the collapsible list below or appendix.

• Baseball statistics abbreviations
  • PA - Plate appearance: number of completed batting appearances
  • HR - Home runs: hits on which the batter successfully touched all four bases, without the contribution of a fielding error
  • R - Runs scored: number of times a player crosses home plate
  • RBI - Run batted in: number of runners who score due to a batters’ action, except when batter grounded into double play or reached on an error
  • SB - Stolen base: number of bases advanced by the runner while the ball is in the possession of the defense
  • ISO - Isolated power: a hitter’s ability to hit for extra bases, calculated by subtracting batting average from slugging percentage
  • BABIP - Batting average on balls in play: frequency at which a batter reaches a base after putting the ball in the field of play. Also a pitching category
  • AVG - Batting average (also abbreviated BA): hits divided by at bats
  • OBP - On-base percentage: times reached base divided by at bats plus walks plus hit by pitch plus sacrifice flies
  • SLG - Slugging average: total bases achieved on hits divided by at-bats
  • wOBA - Some argue that the OPS, on-base plus slugging, formula is flawed and that more weight should be shifted towards OBP (on-base percentage). The statistic wOBA (weighted on-base average) attempts to correct for this.
  • wRC. - Weighted Runs Created (wRC): an improved version of Bill James’ Runs Created statistic, which attempted to quantify a player’s total offensive value and measure it by runs.
  • BsR - Base Runs: Another run estimator, like Runs Created; a favorite of writer Tom Tango
  • WAR - Wins above replacement: a non-standard formula to calculate the number of wins a player contributes to his team over a “replacement-level player”
  • Off - total runs above or below average based on offensive contributions (both batting and baserunning)
  • Def - total runs above or below average based on defensive contributions (fielding and position).

Since the game statistics are in different units we standardize the data by subtracting the mean and dividing by the standard deviation, $x_{changed} = \frac{x-\mu}{s}$. Additionaly, we add two new variables Off.norm and Def.norm which are normalized Off and Def ratings using the formula $x_{changed}=\frac{x-min(x)}{max(x)-min(x)}$. We use the normalized offensive and defensive ratings to quickly evaluate the optimal team according to the ILP.

# select numeric columns and relevant variables
dat.scaled = scale(dat[,sapply(dat, class) == "numeric"][,c(-1:-2,-19)])

# normalize Off and Def
dat$Off.norm = (dat$Off-min(dat$Off))/(max(dat$Off)-min(dat$Off))
dat$Def.norm = (dat$Def-min(dat$Def))/(max(dat$Def)-min(dat$Def))

head(dat.scaled[,1:4])

##              PA         HR          R        RBI
## [1,]  0.9239111  1.2879067  0.7024833  0.4469482
## [2,]  0.6851676  0.6505590  0.4831027  0.8744364
## [3,]  0.6625837  0.4115537  0.0687172  0.7989973
## [4,] -0.9634531 -0.7834733 -0.9306832 -0.9109555
## [5,]  1.1013556  0.5708906  0.6293565  0.8744364
## [6,] -0.9634531 -0.7834733 -0.9306832 -0.9109555

Now that we have scaled player stats we will weigh them and add them up to obtain the player utility index $U_i$ for player $i$ to use it in the objective function.

$U_i(x) = w_{1}\text{PA}_i+w_{2}\text{HR}_i+w_{3}\text{R}_i+w_{4}\text{RBI}_i+w_{5}\text{SB}_i+w_{6}\text{ISO}_i+w_{7}\text{BABIP}_i+w_{8}\text{AVG}_i+w_{9}\text{OBP}_i+w_{10}\text{SLG}_i+w_{11}\text{wOBA}_i+w_{12}\text{wRC.}_i+w_{13}\text{BsR}_i+w_{14}\text{Off}_i+w_{15}\text{Def}_i+w_{16}\text{WAR}_i$

$\text{ for player } i \text{ where } i \in \{1,199\}$

By introducing weights we can construct the weight vector which best suits our preferences. For example, if we wanted the player utility index to value the offensive statistics like RBI more than the defensive statistics like Def we would just assign a bigger weight to RBI. We decided to value each statistic equally, i.e. weights are equal.

Constraint modelling

In baseball there are 25 active men roster and 40 men roster that includes the 25 men active roster. To start a new team we focus on building the perfect 25 men roster. Typically, a 25 men roster will consist of five starting pitchers (SP), seven relief pitchers (Reliever), two catchers (C), six infielders (IN), and five outfielders (OF). Current position variable POS has more than 5 aforementioned groups. We group them in the POS2 variable by the five types SP, Reliever, C, IN, OF.

position = function(x){ # given position x change x to group
  if(x %in% c("1B","2B","3B","SS")) x = "IN"
  else if(x %in% c("Closer")) x = "Reliever"
  else x=as.character(x)
}

dat$POS2 = sapply(dat$POS, position)

Additionally, we will make sure that our 25 men active roster has at least one player of each of the following positions: first base (1B), second base (2B), third base (3B) and Short stop (SS).

There is no salary cap in the Major League Baseball association, but rather a threshold of 189$ million for the 40 men roster for period 2014-2016 beyond which a luxury tax applies. For the first time violators the tax is 22.5% of the amount they were over the threshold. We decided that we would allocate 178$ million for the 25 men roster.

To model the above basic constraints and an objective function we came up with the player utility index $U(x_1,x_2,…,x_n)$ which is a function of the chosen set of $n$ player game statistics, 16 in our case. In our model we maximize the sum of the player utility indices. We have 16 game statistics of interest which are

PA, HR, R, RBI, SB, ISO, BABIP, AVG, OBP, SLG, wOBA, wRC., BsR, Off, Def, WAR, Off.norm, Def.norm

Below is the resulting model.

where

• $U_i$- utility index for player $i$, $i \in \{1,199\}$
• $x_i$ - a binary variable which is one if player $i$ is selected
• $x_{\text{SP}}, x_{\text{Reliever}}$, etc. - binary variables that are one if player $i$ has the specified attribute such as Starting pitcher (SP), left hand pitcher, etc.
• $x_{\text{POS}}$ - binary variable which is one if player $i$ plays the position $POS$, $POS \in \{\text{1B,2B,3B,SS}\}$
• $Stat_{ij}$ - game statistic $j$ for player $i$, $j \in \{1,16\}$
• $mean(Stat_{j})$ - the average of the statistic $j$ across all players
• $salary_i$ - salary for player $i$ in dollars

Constraint (2) ensures that we get 25 players. Constraints (3) through (10) ensure that number of players with certain attributes meets the required minimum. Collection of constraints (11) makes sure that our team’s average game stastistics outperform the average game statistics across all players. Constraint (12) ensures that we stay within our budget including the luxury tax.

Below is the solution of this programm.

library("lpSolve")

i = 199 # number of players (variables)

# constraints
cons = rbind(
  rep(1,i), # 25 man constraint (2)
  sapply(dat$POS2, function(x) if (x == "SP") x=1 else x=0), # (3)
  sapply(dat$POS2, function(x) if (x == "Reliever") x=1 else x=0), # (4)
  sapply(dat$POS2, function(x) if (x == "C") x=1 else x=0), # (5)
  sapply(dat$POS2, function(x) if (x == "IN") x=1 else x=0), # (6)
  sapply(dat$POS2, function(x) if (x == "OF") x=1 else x=0), # (7)
  sapply(dat$POS, function(x) if (x == "1B") x=1 else x=0), # (8)
  sapply(dat$POS, function(x) if (x == "2B") x=1 else x=0), # (8)
  sapply(dat$POS, function(x) if (x == "3B") x=1 else x=0), # (8)
  sapply(dat$POS, function(x) if (x == "SS") x=1 else x=0), # (8)
  sapply(dat$Throws, function(x) if (x == "L") x=1 else x=0), # (9)
  sapply(dat$Bats, function(x) if (x == "L") x=1 else x=0), # (10)
  t(dat[,colnames(dat.scaled)])/25, # (11) outperform the average
  dat$Salary/1000000 # (12) budget constraint
)

# model
f.obj = apply(dat.scaled,1,sum)
f.dir = c("=",rep(">=",27),"<=")
f.rhs = c(25,5,7,2,6,5,2,2,rep(1,4),
          apply(dat[,colnames(dat.scaled)],2,mean),
          178)

model = lp("max", f.obj, cons, f.dir, f.rhs, all.bin=T,compute.sens=1)
model

## Success: the objective function is 135.6201

sol = model$solution
sol

##   [1] 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 0
##  [36] 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
##  [71] 1 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
## [106] 0 0 1 1 0 0 0 1 0 1 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 1 0
## [141] 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
## [176] 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 0 0

Let’s look at our ideal baseball team given the constraints outlined above.

# selected players
dat[which(sol>0),c(1:3,6,28:29)]

##       Salary             Name    POS         Team  Def.norm     POS2
## 4   31000000  Clayton Kershaw     SP              0.3713163       SP
## 8    6083333       Mike Trout     OF       Angels 0.4125737       OF
## 24  19750000      David Price     SP              0.3713163       SP
## 26    507500  Dellin Betances Closer      Yankees 0.3713163 Reliever
## 29    509000       Matt Duffy     2B       Giants 0.5972495       IN
## 53  17142857     Max Scherzer     SP              0.3713163       SP
## 54  17277777     Buster Posey      C       Giants 0.5324165        C
## 62    509500     Carson Smith Closer     Mariners 0.3713163 Reliever
## 71    519500     A.J. Pollock     OF Diamondbacks 0.5422397       OF
## 83    535000 Trevor Rosenthal Closer    Cardinals 0.3713163 Reliever
## 87    547100       Cody Allen Closer      Indians 0.3713163 Reliever
## 108  2500000       Dee Gordon     2B      Marlins 0.5402750       IN
## 109  2500000     Bryce Harper     OF    Nationals 0.2043222       OF
## 113  2725000     Lorenzo Cain     OF       Royals 0.6797642       OF
## 115  3083333 Paul Goldschmidt     1B Diamondbacks 0.2357564       IN
## 119  3200000     Zach Britton Closer      Orioles 0.3713163 Reliever
## 121  3630000     Jake Arrieta     SP              0.3713163       SP
## 129  4300000   Josh Donaldson     3B    Blue Jays 0.5815324       IN
## 139  6000000       Chris Sale     SP              0.3713163       SP
## 142  7000000   Russell Martin      C    Blue Jays 0.6110020        C
## 143  7000000       Wade Davis Closer       Royals 0.3713163 Reliever
## 150  8050000  Aroldis Chapman Closer         Reds 0.3713163 Reliever
## 163 10500000  Yoenis Cespedes     OF        - - - 0.5795678       OF
## 176 14000000       Joey Votto     1B         Reds 0.1886051       IN
## 194   543000  Xander Bogaerts     SS      Red Sox 0.5284872       IN

Seems like a decent team with the mean normalized offensive and defensive ratings of 0.414495 and 0.4275835 respectively. For comparison mean normalized offensive and defensive ratings for all players are 0.3019702 and 0.3821564 respectively. Our team outperforms the average and its mean offensive and defensive ratings are better than $82.9145729$% and $78.3919598$% of other players correspondingly.

While this is a straightforward way to model the selection of the players there are several nuances we need to address. One of them is that the standardized game statistics are not additively independent. As a result, our utility index poorly measures the player’s value and is biased. It is possible to construct an unbiased utility index which has been done a lot in baseball (look up sabermetrics). Off and Defand a lot of other statistics are examples of utility indices. A reddit user suggested a solid way to construct the utility index.

Another issue we need to addrees is when we substituted the missing values with zero. Players with missing game statistics values have their utility index diminished because one of the stats used to calculate it is zero. However, imputing with zero is better than imputing with the mean in our case. By imputing with the mean we would introduce new information into the data which may be misleading, ex. g. a player’s game stat is worse/better than the average. As a result, the player utility index would be overestimated/underestimated.

Finally, I believe that using statistical and mathematical methods is only acceptable as a supplement to the decision making process not only in baseball, but in every field.

Appendix

Baseball statistics abbreviations

• PA - Plate appearance: number of completed batting appearances
• HR - Home runs: hits on which the batter successfully touched all four bases, without the contribution of a fielding error
• R - Runs scored: number of times a player crosses home plate
• RBI - Run batted in: number of runners who score due to a batters’ action, except when batter grounded into double play or reached on an error
• SB - Stolen base: number of bases advanced by the runner while the ball is in the possession of the defense
• ISO - Isolated power: a hitter’s ability to hit for extra bases, calculated by subtracting batting average from slugging percentage
• BABIP - Batting average on balls in play: frequency at which a batter reaches a base after putting the ball in the field of play. Also a pitching category
• AVG - Batting average (also abbreviated BA): hits divided by at bats
• OBP - On-base percentage: times reached base divided by at bats plus walks plus hit by pitch plus sacrifice flies
• SLG - Slugging average: total bases achieved on hits divided by at-bats
• wOBA - Some argue that the OPS, on-base plus slugging, formula is flawed and that more weight should be shifted towards OBP (on-base percentage). The statistic wOBA (weighted on-base average) attempts to correct for this.
• wRC. - Weighted Runs Created (wRC): an improved version of Bill James’ Runs Created statistic, which attempted to quantify a player’s total offensive value and measure it by runs.
• BsR - Base Runs: Another run estimator, like Runs Created; a favorite of writer Tom Tango
• WAR - Wins above replacement: a non-standard formula to calculate the number of wins a player contributes to his team over a “replacement-level player”
• Off - total runs above or below average based on offensive contributions (both batting and baserunning)
• Def - total runs above or below average based on defensive contributions (fielding and position).

Source: Wikipedia::Baseball statistics

Synopsis

Using the U.S. National Oceanic and Atmospheric Administration’s (NOAA) storm database I explore which weather events are most harmful to population health and economy in the US.

Regarding the population health, the most frequent events are usually the most harmful ones such as tornadoes, floods, thunderstorm winds, hurricanes and lightnings. An exception is the excessive heat event which is the 20th most frequent, but the deadliest with 88 deaths per year on average during the 2000-2011 period. Regarding the economy, the most frequent events are not necessarily the most harmful. The first four most harmful economically events are hydro-meteorological events such as floods, hail, storms, hurricanes. During 2000-2011 damage done to property was 14 times greater than the damage done to crops.Below is a detailed analysis.

Data processing

I start with downloading the data, unzipping it, and reading it in.

if(!file.exists("data.csv")) {
  
  if(!file.exists("data.bz2")){
    #Download
    url<-"https://d396qusza40orc.cloudfront.net/repdata%2Fdata%2FStormData.csv.bz2"
    download.file(url,"data.bz2",method="curl")
    }
  
  # Unzip
  zz <- readLines(gzfile("data.bz2"))
  zz <- iconv(zz, "latin1", "ASCII", sub="")
  writeLines(zz, "data.csv")
  rm(zz)
  }

## Read data in
data<-read.csv("data.csv", sep=",", quote = "\"", header=TRUE)

The data set has 902297 observations and 37 variables (columns). Below are the first six rows of the first 5 columns of the data set I am working with as well as the names of all columns.

head(data[,1:5])

##   STATE__           BGN_DATE BGN_TIME TIME_ZONE COUNTY
## 1       1  4/18/1950 0:00:00     0130       CST     97
## 2       1  4/18/1950 0:00:00     0145       CST      3
## 3       1  2/20/1951 0:00:00     1600       CST     57
## 4       1   6/8/1951 0:00:00     0900       CST     89
## 5       1 11/15/1951 0:00:00     1500       CST     43
## 6       1 11/15/1951 0:00:00     2000       CST     77

names(data)

##  [1] "STATE__"    "BGN_DATE"   "BGN_TIME"   "TIME_ZONE"  "COUNTY"    
##  [6] "COUNTYNAME" "STATE"      "EVTYPE"     "BGN_RANGE"  "BGN_AZI"   
## [11] "BGN_LOCATI" "END_DATE"   "END_TIME"   "COUNTY_END" "COUNTYENDN"
## [16] "END_RANGE"  "END_AZI"    "END_LOCATI" "LENGTH"     "WIDTH"     
## [21] "F"          "MAG"        "FATALITIES" "INJURIES"   "PROPDMG"   
## [26] "PROPDMGEXP" "CROPDMG"    "CROPDMGEXP" "WFO"        "STATEOFFIC"
## [31] "ZONENAMES"  "LATITUDE"   "LONGITUDE"  "LATITUDE_E" "LONGITUDE_"
## [36] "REMARKS"    "REFNUM"

For my analysis I needed to extract the year information from the BGN_DATE column.

# Add a new year column to the dataset
data<-data.frame(Year=format(as.Date(data$BGN_DATE,format="%m/%d/%Y"),"%Y"),data)

head(data[,1:5])

##   Year STATE__           BGN_DATE BGN_TIME TIME_ZONE
## 1 1950       1  4/18/1950 0:00:00     0130       CST
## 2 1950       1  4/18/1950 0:00:00     0145       CST
## 3 1951       1  2/20/1951 0:00:00     1600       CST
## 4 1951       1   6/8/1951 0:00:00     0900       CST
## 5 1951       1 11/15/1951 0:00:00     1500       CST
## 6 1951       1 11/15/1951 0:00:00     2000       CST

After looking at the most frequent events I noticed duplicates THUNDERSTORM WIND, THUNDERSTORM WINDS, TSTM WIND, MARINE TSTM WIND. These are the same thing, so I replaced them with TSTM WIND.

# Replace duplicate THUDNDERSTORM WIND, etc. with TTSM WIND
data$EVTYPE = sapply(data$EVTYPE,function(x) gsub("THUNDERSTORM WINDS|MARINE TSTM WIND|THUNDERSTORM WIND","TSTM WIND",x))

The data set has scaling factors for two variables which are needed for analysis. Namely, property damage PROPDMG and crop damage CROPDMG. They have corresponding scaling columns PROPDMGEXP and CROPDMGEXP. The scaling columns contain information about how to scale the values in the columns PROPDMG and CROPDMG. For example, a value in the PROPDMG column that has a scaling factor “k” in the PROPDMGEXP column should be multiplied by $10^3$. I use the following scheme for the scaling factors.

##    Scaling exponent Occurences Scaling factor
## 1                       465934           10^0
## 2                 -          1           10^0
## 3                 ?          8           10^0
## 4                 +          5           10^0
## 5                 0        216           10^0
## 6                 1         25           10^1
## 7                 2         13           10^2
## 8                 3          4           10^3
## 9                 4          4           10^4
## 10                5         28           10^5
## 11                6          4           10^6
## 12                7          5           10^7
## 13                8          1           10^8
## 14                B         40           10^9
## 15                h          1           10^2
## 16                H          6           10^2
## 17                K     424665           10^3
## 18                m          7           10^6
## 19                M      11330           10^6

Some values in the PROPDMG and CROPDMG did not have scaling factors specified or had symbols like +,-,?. I decided not to scale the values that had those symbols. The rest is intuitive, namely, “b” and “B” stand for billion and etc. In the code below I create two new columns, PROPDMGSCALE and CROPDMGSCALE, with property damage and crop damage scaled.

scale.func <- function(x) {
  # Function that replaces a factor with a numeric
   if(x %in% 0:8) {x<-as.numeric(x)}
   else if(x %in% c("b","B")) {x<-10^9}    # billion
   else if(x %in% c("m","M")) {x<-10^6}    # million/mega
   else if(x %in% c("k","K")) {x<-10^3}   # kilo   
   else if(x %in% c("h","H")) {x<-10^2}   # hundred
   else x<-10^0
   }

# Apply scale.func with sapply
data$PROPDMGSCALE <- sapply(data$PROPDMGEXP,scale.func) * data$PROPDMG
data$CROPDMGSCALE <- sapply(data$CROPDMGEXP,scale.func) * data$CROPDMG

I also created a plotting function for horizontal barplots, so I dont have to repeat code:

plot.k<- function(df,title){
  # A function that plots a barplot with presets. Arguments are a matrix-like dataset and a plot title
  barplot(main=title,sort(df,decreasing=FALSE),las=1,horiz=TRUE,cex.names=0.75,col=c("lightblue"))
}

Results

According to the project instructions, with time the recording of the weather events improved. In the multiline graph I show the number of occurences of 10 most frequent weather events by year during 1950-2011. The number of occurences of the events increased drastically due to improvements in the process of recording those events.

# Get table of counts of events by year
dat = as.data.frame(table(data[,c("Year","EVTYPE")]))

# 10 most frequent events
a = sort(apply(table(data[,c("Year","EVTYPE")]),2,sum),decreasing=TRUE)[1:10]
dat = dat[dat$EVTYPE %in% names(a),]

# Modify year column to be in the unambiguos date format %Y-%m-%d
dat$Year = paste0(dat$Year,"-01-01")
dat$Year = as.numeric(as.POSIXct(dat$Year))

# Create Rickshaw graph
# require(devtools)
# install_github('ramnathv/rCharts')
require(rCharts)

r2 <- Rickshaw$new()
r2$layer(
  Freq ~ Year,
  data = dat,
  type = "line",
  groups = "EVTYPE",
  height = 340,
  width = 700
)
# turn on built in features
r2$set(
  hoverDetail = TRUE,
  xAxis = TRUE,
  yAxis = TRUE,
  shelving = FALSE,
  legend = TRUE,
  slider = TRUE,
  highlight = TRUE
)
r2$show('iframesrc', cdn = TRUE)

Below is the list of average occurences per year during 1950-2011 of 20 most frequent events.

# List of average occurences per year
avg_occ = sort(apply(table(data$Year,data$EVTYPE),2,sum),decreasing=TRUE)[1:20]/61
data.frame(`Avg Occurences` = avg_occ)

##                      Avg.Occurences
## TSTM WIND                5401.98361
## HAIL                     4732.14754
## TORNADO                   994.29508
## FLASH FLOOD               889.78689
## FLOOD                     415.18033
## HIGH WIND                 331.34426
## LIGHTNING                 258.26230
## HEAVY SNOW                257.50820
## HEAVY RAIN                192.18033
## WINTER STORM              187.42623
## WINTER WEATHER            115.18033
## FUNNEL CLOUD              112.11475
## MARINE TSTM WIND           95.27869
## WATERSPOUT                 62.22951
## STRONG WIND                58.45902
## URBAN/SML STREAM FLD       55.60656
## WILDFIRE                   45.26230
## BLIZZARD                   44.57377
## DROUGHT                    40.78689
## ICE STORM                  32.88525

In the table below I show the annual averages of property damage, crop damage, total damage, number of injuries, deaths and occurences during 1950-2011. I highlight the time period because later in my analysis I focus on the 2000-2011 period. The table is initially sorted by the average number of occurences per year. You may play around with the table.

# http://rstudio.github.io/DT/
# require(devtools)
# install_github('ramnathv/htmlwidgets')
# install_github("rstudio/DT")

require(htmlwidgets)
require(DT)

# Create data frame for datatable
datatab <- data.frame(
  `Property Damage` = tapply(data$PROPDMGSCALE,list(data$EVTYPE),sum)/61,
  `Crop Damage` = tapply(data$CROPDMGSCALE,list(data$EVTYPE),sum)/61,
  `Total Damage` = 
    tapply(data$PROPDMGSCALE,list(data$EVTYPE),sum)/61 + tapply(data$CROPDMGSCALE,list(data$EVTYPE),sum)/61,
  Deaths = tapply(data$FATALITIES,list(data$EVTYPE),sum)/61,
  Injuries = tapply(data$INJURIES,list(data$EVTYPE),sum)/61,
  Occurences = matrix(table(data[,"EVTYPE"])/61)
  )

# Create datatable initially sorted by avg number of occurences
datatable(format(datatab,big.mark = ',',scientific = F, digits = 1),
          colnames = c('Property Damage,$' = 2, 'Crop Damage,$' = 3, 'Total Damage,$' = 4),
          caption = 'Table: Average annual values, 1950-2011',
          options = list(order = list(list(6, 'desc'))),
          extensions = 'Responsive'
          )

Let’s see whether the most frequent events have a significant effect on the health of population and the infrastructure.

Across the United States, which types of events (as indicated in the EVTYPE variable) are most harmful with respect to population health?

I summarize the number of total injuries and deaths by the event type over the period 1950 to 2011.

# Table of total deaths and injuries by event type during 1950-2011
Tdeaths<-sort(tapply(data$FATALITIES,list(data$EVTYPE),sum),decreasing=TRUE)
Tinj<-sort(tapply(data$INJURIES,list(data$EVTYPE),sum),decreasing=TRUE)

# Total deaths by event type
head(Tdeaths)

##        TORNADO EXCESSIVE HEAT    FLASH FLOOD           HEAT      LIGHTNING 
##           5633           1903            978            937            816 
##      TSTM WIND 
##            710

# Total injuries by event type
head(Tinj)

##        TORNADO      TSTM WIND          FLOOD EXCESSIVE HEAT      LIGHTNING 
##          91346           9361           6789           6525           5230 
##           HEAT 
##           2100

Next, I calculate the average number of deaths and injuries for years 2000-2011. I chose the period 2000-2011 because in the earlier years there are generally fewer events recorded due to poor recording process as was stated in the project instructions. Recent years have more accurate records.

# Boolean to subset data
years<-data$Year %in% 2000:2010

# Average deaths and injuries per year
TdeathsAve<-sort(tapply(data[years,]$FATALITIES,list(data[years,]$EVTYPE),sum),decreasing=TRUE)/11
TinjAve<-sort(tapply(data[years,]$INJURIES,list(data[years,]$EVTYPE),sum),decreasing=TRUE)/11

# Average deaths per year by event type
head(TdeathsAve)

## EXCESSIVE HEAT        TORNADO    FLASH FLOOD      LIGHTNING    RIP CURRENT 
##       88.81818       55.09091       48.36364       40.00000       28.27273 
##          FLOOD 
##       18.90909

# Average injuries per year by event type
head(TinjAve)

##           TORNADO    EXCESSIVE HEAT         LIGHTNING         TSTM WIND 
##         822.72727         324.54545         254.45455         253.45455 
## HURRICANE/TYPHOON          WILDFIRE 
##         115.90909          72.27273

Let’s plot the averages.

par(mfcol=c(1,2))
par(mar=c(3,7,2,3))

rowChart = plot.k(TdeathsAve[1:10],'Avg # of deaths per year')
text(x= sort(TdeathsAve[1:10])+20, y= rowChart, labels=as.character(round(sort(TdeathsAve[1:10]),2)),xpd=TRUE)

rowChart = plot.k(TinjAve[1:10],'Avg # of injuries per year')
text(x= sort(TinjAve[1:10])+200, y= rowChart, labels=as.character(round(sort(TinjAve[1:10]),2)),xpd=TRUE)

par(mfcol=c(1,1))
par(mar=c(5.1,4.1,4.1,2.1))

On average tornados and excessive heat cause the most number of deaths and injuries per year for the period 2000-2011. The most frequent events, tornado, flash flood and thundestorm winds have a significant effect on the population health. However, hail, the second most frequent event, has an insignificant effect on population health. Excessive heat which is 20th most frequent event with $27.06452$ occurences per year is the most deadly. Thus, in general, the events that are most frequent are significantly harmful to the population health. Therefore, countermeasures should be provided on a constant basis. This means that the amortisation and review of the countermeasure infrastructure needs to be frequent as well.

Across the United States, which types of events have the greatest economic consequences?

I calculate the total damage over the period 1950-2011 and average damage for years 2000 to 2011. The total damage is the sum of property damage and the crop damage.

# Total damage table by event type
TtotalDmg<-sort(tapply(data$PROPDMGSCALE,list(data$EVTYPE),sum)
                + tapply(data$CROPDMGSCALE,list(data$EVTYPE),sum)
                ,decreasing=TRUE)

totalDmg = data.frame(row.names = 1:length(TtotalDmg), event = rownames(TtotalDmg),cost = TtotalDmg,`pretty_cost` = format(TtotalDmg,big.mark = ',',scientific = F,digits = 4))

# Show events whose total damage is more than 1bil$ during 1950-2011
totalDmg[totalDmg$cost > 1000000000,c(1,3)]

##                         event        pretty_cost
## 1                       FLOOD 150,319,678,257.00
## 2           HURRICANE/TYPHOON  71,913,712,800.00
## 3                     TORNADO  57,352,115,822.50
## 4                 STORM SURGE  43,323,541,000.00
## 5                        HAIL  18,758,223,268.50
## 6                 FLASH FLOOD  17,562,131,144.30
## 7                     DROUGHT  15,018,672,000.00
## 8                   HURRICANE  14,610,229,010.00
## 9                   TSTM WIND  10,868,962,514.50
## 10                RIVER FLOOD  10,148,404,500.00
## 11                  ICE STORM   8,967,041,560.00
## 12             TROPICAL STORM   8,382,236,550.00
## 13               WINTER STORM   6,715,441,255.00
## 14                  HIGH WIND   5,908,617,595.00
## 15                   WILDFIRE   5,060,586,800.00
## 16           STORM SURGE/TIDE   4,642,038,000.00
## 17             HURRICANE OPAL   3,191,846,000.00
## 18           WILD/FOREST FIRE   3,108,626,330.00
## 19  HEAVY RAIN/SEVERE WEATHER   2,500,000,000.00
## 20 TORNADOES, TSTM WIND, HAIL   1,602,500,000.00
## 21                 HEAVY RAIN   1,427,647,890.00
## 22               EXTREME COLD   1,360,710,400.00
## 23        SEVERE THUNDERSTORM   1,205,560,000.00
## 24               FROST/FREEZE   1,103,566,000.00
## 25                 HEAVY SNOW   1,067,242,257.00

Let’s look at the average total economic damage per year during 2000-2011.

# Average damage per year table for the period 2000-2011 by event type
TtotalDmgAve<-sort(tapply(data[years,]$PROPDMGSCALE,list(data[years,]$EVTYPE),sum)
                + tapply(data[years,]$CROPDMGSCALE,list(data[years,]$EVTYPE),sum),
                decreasing=TRUE)/11

# Turn into a dataframe with pretty cost column
totalDmgAve = data.frame(row.names = 1:length(TtotalDmgAve), event = rownames(TtotalDmgAve),cost = TtotalDmgAve,`pretty_cost` = format(TtotalDmgAve,big.mark = ',',scientific = F,digits = 4))

# Show events whose average total damage is more than 1mil$ per year during 2000-2011
totalDmgAve[totalDmgAve$cost > 1000000,c(1,3)]

##                event       pretty_cost
## 1              FLOOD 11,912,769,002.73
## 2  HURRICANE/TYPHOON  6,537,610,254.55
## 3        STORM SURGE  3,924,630,454.55
## 4               HAIL  1,203,609,870.00
## 5        FLASH FLOOD  1,028,091,082.73
## 6            DROUGHT    904,622,090.91
## 7            TORNADO    894,962,851.82
## 8     TROPICAL STORM    676,727,122.73
## 9          TSTM WIND    516,427,969.09
## 10         HIGH WIND    487,030,401.82
## 11  STORM SURGE/TIDE    418,303,909.09
## 12          WILDFIRE    399,638,581.82
## 13         HURRICANE    315,616,910.00
## 14         ICE STORM    265,541,210.91
## 15  WILD/FOREST FIRE    214,942,875.45
## 16      WINTER STORM    124,723,290.91
## 17      FROST/FREEZE     98,601,454.55
## 18        HEAVY RAIN     76,104,003.64
## 19         LIGHTNING     50,392,913.64
## 20    EXCESSIVE HEAT     45,060,181.82
## 21         LANDSLIDE     29,403,818.18
## 22        HEAVY SNOW     28,213,493.64
## 23       STRONG WIND     18,882,801.82
## 24     COASTAL FLOOD     17,231,505.45
## 25      EXTREME COLD     14,428,000.00
## 26          BLIZZARD     11,092,090.91
## 27           TSUNAMI      8,229,818.18
## 28         HIGH SURF      7,571,136.36
## 29            FREEZE      4,850,000.00
## 30    TSTM WIND/HAIL      4,450,095.45
## 31  LAKE-EFFECT SNOW      3,569,272.73
## 32    WINTER WEATHER      3,086,545.45
## 33  COASTAL FLOODING      1,553,909.09
## 34 EXTREME WINDCHILL      1,545,454.55

Below I plot the average total economic damage per year during 2000-2011 of events whose average economic damage is greater than 1 million.

par(mar=c(2,8,2,6.4))
# Plot average economic damage > than 1mil$ per year during 2000-2011
rowChart = plot.k(totalDmgAve[totalDmgAve$cost > 1000000,]$cost,'Avg Damage per Year in $, 2000-2011')
text(x = sort(totalDmgAve[totalDmgAve$cost > 1000000,2])+1780000000, 
     y = rowChart, 
     labels= format(sort(totalDmgAve[totalDmgAve$cost > 1000000,2]),big.mark = ',',scientific = F,digits = 4),
     xpd=TRUE)

Lastly, let’s look at the average economic damage per year by damage type during 2000-2011. The average annual damage done to property by weather events is 14 times greater than the average annual damage done to crops.

# Average damage per year during 2000-2011 by damage type
format(data.frame(
  prop_dmg=sum(data[years,]$PROPDMGSCALE/11),
  crop_dmg=sum(data[years,]$CROPDMGSCALE/11),
  row.names = '$ annualy'),
big.mark = ',',digits = 4, scientific = F)

##                 prop_dmg      crop_dmg
## $ annualy 28,173,521,423 2,084,491,549

The fact that floods have had the biggest damage in economic terms makes sense. It is a devastating force of nature. Water can crush, water can flow. In the 2000s a bunch of storms and hurricanes took place in the US whose appearences are correlated the floods. However, hurricanes, storms, droughts are not even in the top 16 most frequent events. They are just most devastating to the infrastracture and crops. During 2000-2011 the damage done to property was 14 times greater than the damage done to crops. Therefore, the countermeasures need to focus on ensuring the security of the property.

In undergrad I wrote a tutorial on #Julia programming language in which I analyzed the output of the Collatz function. The Collatz Conjecture was really fascinating to me due to its seemingly simple wording and almost impossible to solve mystery. Since then, #Julia changed significantly, and Terence Tao made a contribution that gets us closer to the proof of the Collatz Conjecture.

View on Julia Notebook nbviewer: https://lnkd.in/eGnHgy2

Update: In September 2019 Tao published a paper in which he proved that the Collatz Conjecture is “almost true” for “almost all numbers.”

Tao’s Paper: https://lnkd.in/eCus8YU

Tao’s Blog Post: https://lnkd.in/eb7ePAu

Table of contents

• Download
• Quick Start
• Dataframes, plotting, and file Input/Output
  • Data frames
  • Plotting data
• Conclusion
• Resources used

Download

Download Julia from http://julialang.org/

Download Julai IDEs:

• Juno from http://junolab.org/

• IJulia kernel for Jyputer notebook from https://github.com/JuliaLang/IJulia.jl

Juno is a good IDE for writing and evaluating julia code quickly. IJulia notebook is good for writing tutorials and reports with julia code results embeded in the document.

Once you’ve installed everything I recommend opening up the Juno IDE and going through the tutorial.

Quick start

I execute all julia code below in Juno. I suggest you create a folder on your desktop and make it your working directory where we will be able to write files. First, a couple of basic commands. To evaluate code in Juno you just need to press Ctrl-D (its in the Juno tutrial):

VERSION # print julia version number

pwd() # print working directory
homedir() # print the default home directory

# cd(pwd()) # set working directory to DirectoryPath

"/Users/kobakhitalishvili"

3+5 # => 8
5*7 # => 35
3^17 # => 129140163
3^(1+3im) # im stands for imaginary number => -2.964383781426573 - 0.46089998526262876im
log(7) # natural log of 7 => 1.9459101490553132

1.9459101490553132

1.9459101490553132

Interesting that julia has imaginary number built in. Now, variables and functions:

a = cos(pi) + im * sin(pi) # assigning to a variable

-1.0 + 1.2246467991473532e-16im

b = ℯ^(im*pi)

-1.0 + 1.2246467991473532e-16im

a == b # boolean expression. It is an euler identity.

true

Lets see how to define functions. Here is a chapter on functions in julia docs for more info.

plus2(x) = x + 2 # a compact way

function plustwo(x) # traditional function definition
    return x+2
end

plustwo (generic function with 1 method)

plus2(11)

13

plustwo(11)

13

Here is a julia cheatsheet with above and additional information in a concise form. Next, lets write a function that will generate some data which we will write to a csv file, plot, and save the plot.

Data frames, plotting, and file Input/Output

I decided to write a function $f(x)$ that performs the process from the Collatz conjecture. Basically, for any positive integer $x$ if $x$ is even divide by $2$, if x is odd multiply by $3$ and add $1$. Repeat the process until you reach one. The Collatz conjecture proposes that regardless of what number you start with you will always reach one. Here it is in explicit form

The function collatz(x) will count the number of iterations it took for the starting number to reach $1$.

function collatz(x)
    # Given a number x
    # - divide by 2 if x is even
    # - multiply by 3 and add 1 if x is odd
    # until x reaches 1
    # Args:
    # - param x: integer
    # - return: integer
    count = 0
    while x != 1
        if x % 2 == 0
            x = x/2
            count += 1
        else
            x = 3*x + 1
            count += 1
        end
    end
    return count
end

collatz(2)

1

collatz(3)

3

Data frames

Now, let’s create a dataframe with the number of steps needed to complete the Collatz process for each number from 1 to 1000. We will use the DataFrames package because the base julia library does not have dataframes.

# install DataFrames package
using Pkg
# Pkg.add("DataFrames")

using DataFrames

# Before populating the dataframe with collatz data lets see how to create one
df = DataFrame(Col1 = 1:10, Col2 = ["a","b","c","d","e","f","a","b","c","d"])
df

10 rows × 2 columns

# Neat. Now let's generate data using collatz function
df = DataFrame(Number = 1:1000, NumofSteps = map(collatz,1:1000))
first(df, 10)

10 rows × 2 columns

map() applies collatz() function to every number in the 1:1000 array which is an array of numbers [1,2,3,...,1000]. In this instance map() returns an array of numbers that is the output of collatz() function.

# To get descriptive statistics 
describe(df)

2 rows × 8 columns

Before we save it lets categorize the points based on whether the original number is even or odd.

df.evenodd = map(x -> if x % 2 == 0 "even" else "odd" end, 1:1000) # create new evenodd column
# rename!(df, :x1, :evenodd) #rename it to evenodd
first(df,5)

5 rows × 3 columns

I use the map() function with an anonymous function x -> if x % 2 == 0 "even" else "odd" end which checks for divisibility by 2 to create a column with “even” and “odd” as entries. Finally, I rename the new column “evenodd”.

Additionally, let’s identify the prime numbers as well.

# Pkg.add("Primes")
using Primes

isprime(3)

true

df.isprime = map(x -> if isprime(x) "yes" else "no" end,df.Number)
first(df,5)

5 rows × 4 columns

# Pkg.add("CSV")
using CSV

# To save the data frame in the working directory 
CSV.write("collatz.csv", df)

"collatz.csv"

Plotting data

To plot the data we will use the Gadfly package. Gadly resembles ggplot in its functionality. There is also the Plots package which brings mutliple plotting libraries into a single API.

To save plots in different image formats we will need the Cairo pakage.

# Pkg.add(["Cairo","Fontconfig","Plots", "Gadfly","PlotlyJS","ORCA"])
# Pkg.add("Gadfly")

# using Plots
# plotlyjs() use plotly backend
# pyplot() use pyplot backend
using Cairo
using Gadfly

Gadfly.plot(df,x=:Number, y=:NumofSteps, Geom.point, Guide.title("Collatz Conjecture"))

<?xml version=”1.0” encoding=”UTF-8”?>